就活生の最初の関門。それがWEBテストです。どれも難しいですが、特にSPI非言語は他よりも文章量が多いうえに時間が短く、制限時間内に解ききれない人も多いです。
実際僕も就活を始めたての大学3年の頃は、全くSPIで点数を取ることができず、大手のインターンに悉く落ちていました。「WEBテストさえできたら、絶対面接に通る自信はあるのに！」と唇を噛み締めながら、お祈りメールを眺めていた思い出があります。
この記事を読んでいる人の中にも僕のように悔しい思いをしている人がいるのではないでしょうか。しかしそんなあなたも諦める必要はありません。SPI非言語が全くできなかった僕でも、この記事でお伝えする勉強法を行うことで、大手コンサルや大手メーカーのSPIを通過することができました。
この記事を読めば、SPI非言語のキホンが理解できるだけでなく、苦手な人でも効率的に勉強を進める方法がわかります。ぜひ最後まで読んでみてください。
この記事でわかること
- SPI非言語を時間内に解けない人
- 周りのみんながSPIに通過しているのに、自分は通過できていなくて焦っている人
- SPI非言語を短期間で効率よく対策したいと思っている人
基本的にSPIは結果が確認することのできないですが、SPI体験模試では各分野の結果を確認することができます！
「SPIの模試を受けたい」「SPIの結果を確認したい」と感じた方は、「SPI体験模試」に挑戦してみることをおすすめします！
SPI体験模試では、
- 本番同様の時間制限下で解ける
- 適性検査の結果から自分の実力がわかる
- 各問題の解説がじっくり見られる
など、結果を確認できるからこそ、あなたの就活を効率的に進めることができます。
「SPI体験模試」はこちらから！
SPI体験模試はこちら
SPI非言語のキホンを知ろう
敵を倒すには、まず敵を知らなければいけません。この章では、SPI非言語の基礎知識をお伝えします。知らなかった人はおさらいしておきましょう。
【SPI非言語】出題分野と頻出度
SPI非言語の出題分野を下の図にまとめてみました。
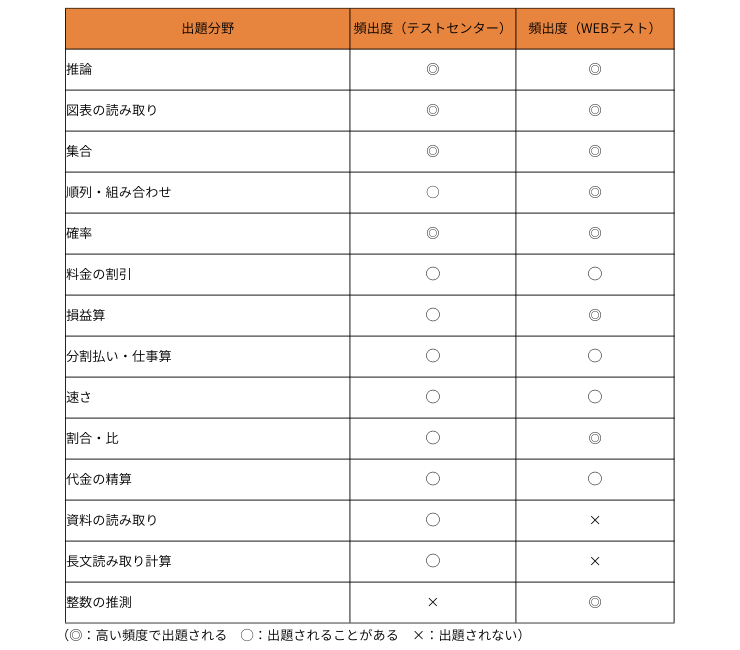
特に頻出度の高い「推論」と「順列・組み合わせ」は難易度が高く、回答に時間がかかってしまいがちです。演習を積み重ねて、どんなパターンでも対応できるようにしておきましょう。
【SPI非言語】問題数
SPI非言語の問題数をまとめた図は次のようになります。受験方法によって異なるため注意しましょう。
【SPI非言語】大手のボーダーライン
SPIは大量の学生を一度に精査できることから、人気企業で採用されています。下にボーダーの正答率を業界ごとにまとめたので、参考にしてみてください。
外資系コンサルなどの超人気企業のボーダーラインが高いことはいわずもがなですが、いずれにせよ大手に入社したいのであれば、ボーダー60％を突破することは必須です。下の記事で、有名企業のボーダー一覧をご紹介しているので、ぜひ参考にしてみてください。
【例題】SPI非言語の分野別の解き方
推論
SPIの推論は問題文で与えられる情報から解答を導き出す問題のことです。推論では、論理的思考力や問題解決能力があるかどうかを測られます。
推論の問題を解く際には下記を徹底しましょう。
- 必ず紙に書く
推論の問題は情報量が多いため、頭の中だけで処理するのは難しいです。そのため、図や表で可視化して矛盾しているポイントや規則に早く気付けるようにしましょう。 - 完璧よりもスピード重視
30秒考えて、規則が見えてこなければ飛ばしましょう。明確に飛ばすルールを設けておくことで、時間を無駄にせず解くことできます - 同じ問題を最低でも3回解き直す
SPIの推論の問題はある程度パターン化されています。しかし、それを体系的に理解して実践に移すよりも、何度も解いて反射的に解けるようになる方が早いです。
例題
Aさん、Bさん、Cさん、Dさんの4人の会社員がいる。業務について以下のことがわかっている。
条件:
1. AとCは同じ日に外回りに出ない
2. Bが外回りに出る日は必ずDも出る
3. Dが出ない日は必ずCが出る
「Aさんが外回りに出る日」に誰が必ず一緒に出るか。
選択肢
ア. A・B
イ. A・C
ウ. A・D
エ. A・B・C
解答：ウ
解説
1. Aが出る日を前提にする
→ 条件1.より「AとCは同じ日に出ない」から、Cはその日は出られない。
→ よって、Cは不参加確定。
2. Dについて考える
• 仮にDが出ないとすると、条件3より「Dが出ない日は必ずCが出る」必要がある。
• でも、AとCは同時に出られないので矛盾する。
• したがって、Aが出る日にはDも必ず出る。
3. Bについて考える
• Bは出ても出なくてもよいが、もし出るなら条件2によりDも出る必要がある。
• すでにDが出ることは確定しているので、Bが出ても矛盾しない。
• ただし「必ずBが出る」わけではないので、Bは任意。
推論の問題をもっと解きたい人はこちらから！
場合の数
場合の数は「2個のサイコロの出目の組み合わせ」のような、ある事柄が起こりうつ場合の数のことを指します。
場合の数の問題を解く際には下記の公式を覚えておきましょう。
- 異なるn個の並べ方：n! = n × (n – 1) × ⋯ × 3 × 2 × 1
例：4! = 4×3×2×1 = 24 - 異なるn個からr個を並べる：nPr = n × (n – 1) × ⋯ × (r + 1) ×r
例：4P2 = 4×3 = 12 - 異なるn個からr個組み合わせ：nCr = nPr ÷ r!
例：5C2 = (5×4) ÷ (2×1) = 10
例題
5人の学生（A, B, C, D, E）が横一列に並びます。
このとき、AとBが必ず隣同士に並ぶ場合の並び方は何通りあるでしょうか。
解答：48通り
解説
隣接する位置の組は「1-2, 2-3, 3-4, 4-5」の 4通り
→その中で AB/BA の2通り
→残り3人（C,D,E）を他の3枠に 3! = 6通り → 4 × 2 × 6 = 48通り
場合の数の問題をもっと解きたい人はこちらから！
割合と比
割合と比の問題では、売上の増加額や去年と今年の来場数の差を求めるような問題が出されます。
割合と比の問題では以下の公式を暗記しておきましょう。
- 割合(%) = (部分 ÷ 全体) ×100
例：人口が1000人の町に200人の男性がいる場合の男性の割合
(200 ÷ 1000) × 100 = 20(%) - 20%増加：1.2をかける
例：1000人の来場者数から20％増加した
1000 × 1.2 = 1200(人)
例題
ある映画館の来場者は合計720人で、男性は全体の55%、女性は45%であった。
さらに男性のうち20歳未満は全体の15%、女性のうち20歳未満は全体の10%である。
20歳以上の女性の人数は何人か。（小数点）
解答：252通り
解説
今回は女性の人数を聞かれているので、男性の情報は無視して構いません。与えられている必要な情報を整理すると以下の通りになります。
- 女性は全体の45%→ 720 × 0.45 = 324(人)
- 20歳未満の女性は全体の10％→ 720 × 0.10 = 72(人)
20歳以上の女性は女性の全人数からから20歳未満の人数を引けばよいので、
324 – 72 = 252
となり、答えは252人になります。
損益算
損益算とは品物の定価や原価、それを売り出したときの利益などを求める問題です。
「原価 → 定価 → 実際の売値 → 利益」 の関係を正しく整理できるかがカギとなります。
以下の3つの公式を覚えておきましょう。
- 定価 = 原価 × (1 + 利益率)
- 売上 = 売値 × 個数
- 総利益 = 総売上 − 総原価 （原価に基づく計算で確認するとミスが減る）
ある文具店が、原価500円のノートを600冊仕入れた。
原価の3割の利益が出るように定価をつけたところ、販売期間中に400冊しか売れなかった。
そこで残りのノートは定価の25%引きにしてすべて売り切った。
このとき、文具店が得た合計利益はいくらか。
解答：57,500円
解説
合計利益 = 総売上 – 総原価 なので、総売上と総原価を出せば答えは出ます。
総売上 = 400 × (500 × 1.3) + 200 × (500 × 1.3 × (1 – 0.25))
= 357,500円
総原価 = 600 × 500 = 300,000円
したがって、答えは357,000円 – 300,000円 = 57,500円 となります。
損益算の問題をもっと解きたい人はこちらから！
料金割引
料金割引は金額の割引率に応じて、最終的にいくらになるかを求めるような問題がよく出題されます。考え方は損益算とほぼ同様になります。
以下の公式を覚えておきましょう。
- 値引き後の価格 = 価格 × (1 – 割引率)
- 総額 = 価格 × 個数
あるゲームセンターの利用料金は1時間あたり400円です。ただし、2時間目以降は常に20%引きとなります。
このゲームを 3時間利用したとき、合計の料金はいくらでしょうか。
解答：1,040円
解説
1時間目：400円（割引なし）
2,3時間目：400 × (1 – 0.2) = 320円
合計すると、400 + 320 + 320 = 1,040円
料金割引の問題をもっと解きたい人はこちらから！
仕事算
仕事算とは、「作業を1人で行うと何時間かかる」といった条件から、複数人で作業を行ったときや、給水と排水が同時に行われたときに、作業が完了するまでの時間や量を求めるような問題です。
※物理や理科で出る仕事とは異なるので注意してください。
以下の内容を理解して、例題を解いてみましょう。
- 1仕事＝1 として「1時間あたりの仕事量」に変換する
- 複数人は足す、逆作業は引く
- 最後に「1 ÷ 正味の仕事量」で時間を求める
Cさん1人では12日間、Dさん1人では18日間で終わる仕事がある。この仕事を2人で4日間行い、残りをDさん1人で行った。この仕事を仕上げるまでに合わせて何日かかったか。
解説
この仕事を1として考えましょう。
2人で4日間やった仕事を最初に求めて、Dさんが1人でやった仕事量を求めます。
一日で進む仕事量：4 × (1/12 + 1/18) =5/9
→残りの仕事は1 – 5/9 = 4/9
次に、残った仕事を Dさんが仕上げるまで何日かかるかを求めます。
4/9 ÷ (1/18) = 4/9 ×18 = 8(日)
したがって、仕事を終えるまでには 4 + 8 = 12(日)かかります。
仕事算の問題をもっと解きたい人はこちらから！
代金精算
代金精算の問題をもっと解きたい人はこちらから！
速度算
速度算とは、「速さ・時間・距離」の関係を利用して、移動や出会い・追いつきに関する問題を解くものです。「往復・休憩・出会い・追いつき」など様々なバリエーションがありますが、基本はシンプルな関係式に落とし込めます。
下記の公式はすべての問題で使用するので、確実に覚えておきましょう。
- 時間 = 距離 ÷ 速さ
- 距離 = 速さ × 時間
- 速さ = 距離 ÷ 時間
例題
ある人が川沿いの道を往復した。
行きは時速 6 km、帰りは時速 9 km で歩き、途中で 15分 休憩した。
往復にかかった時間は休憩を含めてちょうど 2時間 だった。
休憩時間を除いた移動の平均時速は次のうちどれか。
選択肢
A. 6.6 km/h
B. 7.2 km/h
C. 7.5 km/h
D. 8.0 km/h
解答：B
平均時速 = (移動した距離) ÷ (移動していた時間) なので、移動した距離と移動していた時間を求めればよいです。移動していた時間は2時間から休憩時間を抜いた時間なので、1時間45分すなわち1.75時間です。
また、川沿いの道の長さをxとすると、移動していた時間について、以下の式が成り立ちます。
(x/6) + (x/9) = 1.75
これを解くと x = 6.3 kmとなります。移動した距離はこの2倍なので、
平均時速 = (2 × 6.3) / 1.75 = 7.5km/h となります。
速度算の問題をもっと解きたい人はこちらから！
集合
集合算は「Aが当てはまる人」「Bが当てはまる人」「両方/どちらでもない」を数えるような問題です。集合算でいちばん重要なのは、頭の中で考えずに下記のようなベン図を描いてから計算することです。
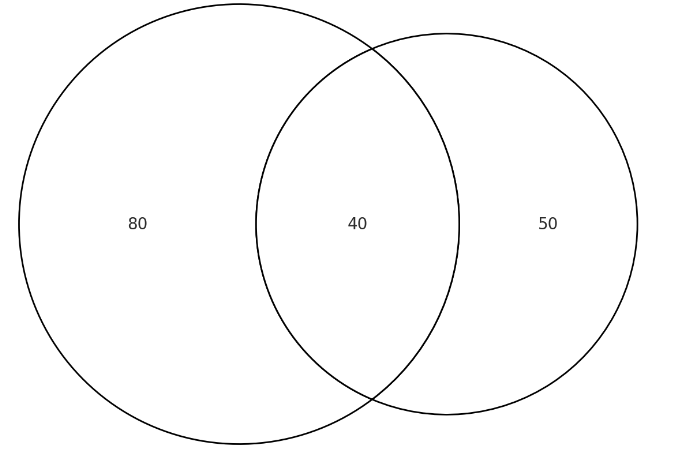
また、その上で下記の公式は暗記しておきましょう。計算がスムーズになります。
- |A∪B| = |A| + |B| – |A∩B|
- 片方だけ Aのみ = |A| – |A∩B| Bのみ = |B| – |A∩B| どちらか一方だけ = |A| + |B| – 2|A∩B|
- どちらでもない どちらでもない = \text{全体} – |A∪B|
※ ∪→または, ∩→かつ
ある学園祭の来場者についてアンケートを行った。
企画Aを体験した人は全体の50%、企画Bを体験した人は全体の40%、両方を体験した人は全体の20%であった。
また、どちらの企画も体験していない人は120人であった。
どちらか一方のみを体験した人は何人か。
解答：120人
解説
最初にどちらか一方のみを体験した人の割合を求めます。
Aのみ： |A| – |A∩B| = 50% – 20% = 30%
Bのみ：|B| – |A∩B| = 40% – 20% = 20%
したがって、全体の50％の人がどちらか片方のみを体験した人です。
次に全体の人数を求めます。
どちらも体験していない人は120人で、その割合は1つ目の公式から
50% + 40% – 20% = 30% とわかります。
したがって、全体の人数は120 ÷ 0.3 = 400人となります。
これらを合わせると、400 × 0.5 = 200人となります。
集合の問題をもっと解きたい人はこちらから！
確率
確率の問題に苦手意識がある人も多いのではないでしょうか。確率の基本は全体を計算して、求める事象が起きる数を計算することです。
また、苦手意識がある人は反復して練習をして、正解率を高めていきましょう！
袋の中に赤玉4個、白玉3個、青玉3個の合計10個が入っている。
ここからAさんとBさんが1個ずつ順に取り出す（戻さない）。
Aさんが赤玉、Bさんが白玉を取り出す確率を分数で答えよ。
解答：2/15
解説
まずは全体の場合の数を求めましょう。
Aさんは10個から1つ選ぶので10通り、Aさんが選んだ玉は戻さないため、Bさんは9個から1つ選ぶので9通りです。
したがって、全体の数は 10 × 9 = 90通りです。
次にAさんが赤玉、Bさんが白玉を取り出す場合の数を求めます。
Aさんが赤玉を取り出す場合の数は4通り、Bさんが白玉を取り出す確率は3通りです。
したがって、Aさんが赤玉、Bさんが白玉を取り出す場合の数は4 × 3 = 12通りです。
これらを合わせると求める確率は 12/90 = 2/15となります。
確率の問題をもっと解きたい人はこちらから！
時間がない人でも大丈夫。SPI非言語の対策を効率的に進める方法
それでは、どうやってSPI非言語の勉強を進めていけばよいのでしょうか？ここではSPI弱者だった僕が、効率的にSPI非言語を対策し、大手コンサルや大手メーカーのSPIを通過することができた勉強法をご紹介します。
①問題集を買う
この勉強法では、問題集が必要になります。下の記事では「1から丁寧に始めたい人」から「選考まで時間がない人」まで様々なレベル、状況にあった問題集をご紹介しています。この記事を参考に自分にあったSPIの問題集を探してみてください。
②苦手分野を見つける
問題集を用意できたら、まず非言語の問題を1問1分で解き、間違えた問題にチェックをつけていきましょう。こうすることで、俯瞰的に自分がどの分野に弱いのかを知ることができます。
よく「時間をかけたら解ける」と言って、時間を測らない人がいますが、本番で制限時間内に解けなければ0点です。自分の実力を知るためにも必ずタイマーをセットするようにしましょう。
ただ、試験が1、2週間後に迫っているという方は300ページ以上もある問題集を一から解く時間なんてないですよね。。。僕にもそんな余裕はありませんでした。そんな方はぜひSPIマスターに申し込んでみてください！
SPIマスターは本番と全く同じ形式のSPIを無料で受験することができるだけでなく、試験結果を受け取ることができるため、自分の苦手分野を簡単に見つけることができます。
さらに、受験後の面談で、キャリアアドバイザーがこれから苦手分野を克服するためのアクションプランを一緒に練ってくれるため、一人で勉強できないという就活生にもおすすめです。下の「SPIマスターを申し込む」をクリックして、利用してみてください！
③間違えた原因を分析する
問題集やSPIマスターで苦手分野を特定できたら、次は間違えた原因を分析しましょう。考えられる主な原因は次の2つです。
- そもそも解法がわからない
- 時間が足りない
「1．そもそも解法がわからない」場合は、入念に問題集の解説を読み込み、みなくても同じ思考が辿れるまで解き直しましょう。
「2．時間が足りない場合」は、どうように解説を読んでより速い計算方法がないか模索しましょう。自宅で受験するWEBテストの場合は、電卓も使えるため、メモリー（M）などマイナーではありつつ、計算スピードの向上できるコマンドを覚えるのも1つの手です。
④学びをノート／ドキュメントにまとめておく
問題集での演習は、あっているか間違っているかは差して重要ではありません。何ができないのかを知り、次につなげることが目的です。そのため、ノートやドキュメントに、同じパターンの問題に出くわした際に、どう行動すればよいのかをまとめておきましょう。
僕の場合、例えば次のように学びをまとめていました。
- 推論：解法がわかっても一度立ち止まり、前提となっている数値の範囲を考える
- 集合：べン図は同じものを使いまわすと、どの数字がどの部分を表しているのかわかりにくくなるので、問いごとに書き直す
⑤次の日に解き直す
学びをまとめて、満足してはいけません。次の日に同じ問題を解き直す。これが一番重要です。 なるべく時間をあけずに復習することで、記憶の定着率は上がります。
時間を空けて復習すると、前回解いた問題なのに解けなくなっているということが僕にも頻繁にありました。そうすると、ふりだしに戻ってしまい、進歩が感じられないため、効率的でない上にモチベーションも下がってしまいます。
だからこそ、次の問題にいきたい気持ちをグッと抑えて、前の日の復習をすることが肝要です。
押えておきたいSPI非言語の公式一覧
上記の手順で実践を積むことが重要なのは自明ですが、同様に基本的な公式を覚えておくことも重要です。公式を覚えることで、思考時間が短縮され、よりスピーディーに問題を解くことができます。
| カテゴリー | 項目 | 式 |
|---|---|---|
| 速さ・時間・距離 | 速さ | 速さ = 距離 ÷ 時間 |
| 速さ・時間・距離 | 時間 | 時間 = 距離 ÷ 速さ |
| 速さ・時間・距離 | 距離 | 距離 = 速さ × 時間 |
| 割合・比 | 割合 | 割合 = 比べる量 ÷ 元の量 |
| 割合・比 | 比べる量 | 比べる量 = 元の量 × 割合 |
| 割合・比 | 元の量 | 元の量 = 比べる量 ÷ 割合 |
| 割合・比 | 比の関係 | a : b = A : B |
| 割合・比 | 内項と外項の関係 | 内項の積 = 外項の積（b×A＝a×B） |
| 確率 | 確率 | 確率 = 望ましい結果の数 ÷ 全ての結果の数 |
| 場合の数（順列・組み合わせ） | 順列 | 順列 = nPr |
| 場合の数（順列・組み合わせ） | 組み合わせ | 組み合わせ = nCr |
| 集合 | 2つの集合 | |A∪B| = |A| + |B| − |A∩B| |
| 集合 | 3つの集合 | |A∪B∪C| = |A| + |B| + |C| − |A∩B| − |B∩C| − |C∩A| + |A∩B∩C| |
| 料金 | 総額 | 単価 × 数量 = 総額 |
| 損益算 | 原価 | 原価 = 仕入れにかかった金額 |
| 損益算 | 売価 | 売価 = 売った金額（原価＋利益） |
| 損益算 | 利益 | 利益 = 売価 − 原価 |
| 損益算 | 損失 | 損失 = 原価 − 売価 |
| 損益算 | 利益率 | 利益率 = 利益 ÷ 原価 × 100 |
| 損益算 | 損失率 | 損失率 = 損失 ÷ 原価 × 100 |
| 仕事算 | 仕事量 | 仕事量 = 仕事率 × 時間 |
| 仕事算 | 1時間あたりの仕事率 | 1時間あたりの仕事率 = 1 ÷ 作業時間 |
| 分割払い | 総支払額（利息あり） | 総支払額（利息あり） = 商品価格＋利息 |
| 分割払い | 利息 | 利息 = 商品価格 × 年利率 × 支払期間 |
| 分割払い | 月々の支払額（利息なし） | 月々の支払額（利息なし） = 総額 ÷ 支払回数 |
| 分割払い | 月々の支払額（利息あり） | 月々の支払額（利息あり） = 総支払額 ÷ 支払回数 |
下の記事ではSPI非言語の公式とよく出る練習問題をより詳しく紹介しているのでぜひチェックしてみてください。
SPI非言語に関するFAQ
Q. SPI非言語で高得点か判別する方法ってあるの？
SPI非言語で高得点かを見分ける方法は次の3つです。
- 表の読み取り問題のタブ数：通常、表の読み取り問題は2つのタブ（小問）で構成されていますが、正答率が高い場合、4つのタブが出現することがあります。
- 推論問題の出題数：推論問題は非言語分野で最も難易度が高いとされ、これが複数回出題される場合、高得点を取れている可能性が高いです。
- 推論問題の形式：推論問題がチェックボックス形式（複数選択）で出題される場合、難易度が高く、高得点を期待できます。
Q．SPI非言語はいつから勉強するべき？
SPI非言語の対策は、本番の3ヶ月ほど前から勉強し始めるのがベストです。もともと数学な得意な人は、1週間前に問題集を1周するだけで問題ないかもしれませんが、苦手な人はできるだけ早くからはじめておくべきです。
ただ、本番まで全く時間がないという方は、SPIマスターを使って効率よく苦手分野を発見し、すぐに弱点の補強に努めましょう。
Q．SPI非言語はどのくらいの頻度で勉強すべき？
SPI非言語は毎日勉強するのが好ましいです。理由は先ほども言ったように、反復学習をした方が記憶の定着率が高いからです。
まとめ
最後にこの記事のまとめです。
- SPI非言語でつまずくのは、私立文系。数学を長い間勉強していないなら、難しいと思うのは当たり前
- SPI非言語の勉強は、「苦手分野の発見」「原因の分析」「ノートに学びをまとめる」「次の日に解き直す」の順番で進めていこう
- 時間がない人はSPIマスターを使ってすぐに苦手分野を発見し、キャリアアドバイザーと目標までの学習計画を立てて効率的に勉強しよう
基本的にSPIは結果が確認することのできないですが、SPI体験模試では各分野の結果を確認することができます！
「SPIの模試を受けたい」「SPIの結果を確認したい」と感じた方は、「SPI体験模試」に挑戦してみることをおすすめします！
SPI体験模試では、
- 本番同様の時間制限下で解ける
- 適性検査の結果から自分の実力がわかる
- 各問題の解説がじっくり見られる
など、結果を確認できるからこそ、あなたの就活を効率的に進めることができます。
「SPI体験模試」はこちらから！
SPI体験模試はこちら