SPIの非言語(数学)、「難しすぎる!」って焦っていませんか?
勉強しても時間が足りなかったり、そもそも問題の意味がわからなかったり…。
でも大丈夫、SPIの非言語は「解き方のコツ」さえ掴めば、必ず点数が上がる分野です。
この記事では、非言語が難しい理由から、全10分野の例題と解き方、具体的な対策法まで、あなたの不安がなくなるまで徹底的に解説しますね。
こんな人に読んでほしい
- SPIの非言語に「ボロボロだ…」と落ち込んでいる人
- 数学から長く離れていて、公式なんて覚えていない!という人
- 効率的な勉強法がわからず、何から手をつけていいか迷っている人
「SPI非言語難しすぎる」就活生の声

まずは、あなたと同じようにSPI非言語に悩む就活生の声を、知恵袋やX(旧Twitter)から集めてみました。
決してあなた一人だけが悩んでいるわけではないので、安心してください。
「そもそも中学数学の公式を忘れた」
「推論の問題、文章がややこしくて何を問われているのか理解できない」
「一問に1分とか無理。時間が圧倒的に足りない」
「青い問題集(高難易度)を買ったら、難しすぎて挫折した」
「数学アレルギーだから、非言語って聞くだけでキツイ」
このように、「苦手意識」「時間不足」「問題の特殊性」の3点でつまずいている人が多いようです。
学校のテストとは違う、SPI特有の「難しさ」があるんですね。
SPI非言語が難しすぎるのはなぜ?

では、なぜ多くの就活生がSPI非言語を「難しすぎる」と感じてしまうのでしょうか?
その主な理由を3つに分けて、深掘りしていきます。
制限時間が短いから
最大の理由は、「圧倒的な時間不足」です。
非言語の試験時間は約35分で、30問前後を解かなければなりません。
単純計算で、1問あたりにかけられる時間はたったの1分程度。
「えーっと、この問題はどう解くんだっけ…」と考えている間に、タイムアップになってしまいます。
このスピード感は、じっくり考えて解く学校のテストとは全く別物です。
解き方を瞬時に思い出し、すぐに計算を始める瞬発力が求められるため、多くの人が「難しい」と感じるのです。
「論理整理力」が問われるから
SPIの非言語は、単なる計算問題だけではありません。
特に「推論」や「集合」といった分野では、日常生活ではあまり触れないタイプの情報処理が求められます。そのため慣れていない人にとっては、「そもそもどう考えればいいのか」がつかみにくい形式になっているんです。
問題文がわざと複雑に書かれていることも多く、その内容を文章として捉え、必要な条件だけを抜き出して整理する力が必要になります。
「数学が苦手」というより、普段使わない思考の枠組みで考えることに慣れていない人がつまずきやすい分野と言えるでしょう。
情報を図や表に書き出して整理する練習ができていないと、頭の中だけで処理しようとして混乱しやすくなってしまいます。
出題範囲が広いから
SPI非言語の出題範囲は、なんと中学〜高校レベルと非常に広範囲です。
損益算、速度算、仕事算、確率、場合の数、集合…。
「あ、この言葉聞いたことある…」と思っても、「じゃあ公式は?」と聞かれると思い出せないものが多くありませんか?
大学受験で数学を使わなかった文系の学生にとっては、忘れていて当然です。
この広い範囲の公式や解法パターンを、ゼロから思い出して対策する必要があるため、勉強を始めるハードルがとても高く感じてしまうのです。
【難しすぎる?】SPI非言語の出題分野と例題

出題範囲が広い、と言われてもピンとこないかもしれませんね。
ここでは、非言語の主要10分野について、それぞれ「どんな問題か」「どう解くか」を例題付きで見ていきましょう!
推論
SPI非言語の「推論」では、与えられた条件を正確に整理し、論理的に結論を導く力が試されます。
数式よりも文章で考えるタイプの問題が多く、読解力と分析力の両方が必要です。
例題
「Aさん、Bさん、Cさん、Dさんの4人がテストを受けました。
AさんはBさんより点数が高く、CさんはDさんより低い。
Bさんの点数はCさんより高い。
このとき、2番目に高い点数の人は誰ですか?」
条件を整理すると、A>B、D>C、B>Cの関係があります。
まずCが最下位とわかります。
次に、AはBより上、DはCより上なので、Dの位置をAとBの間に置くと全体が整います。
結果として点数の順はA>D>B>Cとなり、2番目に高いのはDさんです。
このように、条件を不等号(>、<)や図で書き出し、可視化することが重要です。
「AはBより上」なら「A>B」と、情報を一つずつ丁寧に整理する癖をつけましょう。
詳しい解法やココシロのオリジナル練習問題は次の記事で紹介しています!
確率
「確率」は、ある事象が起こる可能性を数値で表す問題です。
SPIでは高頻度で出題されますが、パターンは限られています。
「(当てはまる場合の数)÷(すべての場合の数)」という基本さえ押さえれば大丈夫です。
例題
「A、B、C、D、Eの5人が横一列に並ぶとき、AとBが隣り合う確率はどれくらいか?」
まず「すべての場合の数」を求めます。5人が自由に並ぶ方法は「5の階乗(5!)」です。
5 × 4 × 3 × 2 × 1 = 120通り。これが分母になります。
次に「AとBが隣り合う場合の数」を求めます。「AとB」を1つのカタマリとして(AB)と見ます。
すると、(AB)、C、D、Eの4つを並べることになるので「4の階乗(4!)」です。
4 × 3 × 2 × 1 = 24通り。
さらに、カタマリの中で「AとB」が「BとA」になる場合もあるので、24通り × 2 = 48通り。これが分子です。
よって確率は 48 ÷ 120 = 2/5 となります。
「すべての場合の数(分母)」と「当てはまる場合の数(分子)」を分けて考えるのが鉄則です。
「隣り合う」なら「カタマリにする」、「同時に」なら「組み合わせ(C)」など、特有の解法パターンを覚えましょう。
場合の数
「場合の数」は、「全部で何通りのパターンがあるか」を計算する問題です。
「順列(P)」=順番を考慮する、「組み合わせ(C)」=順番を考慮しない、という違いを理解することがスタートラインです。
例題
「6人の学生の中から、リレーの第1走者、第2走者、アンカー(第3走者)を選ぶ方法は何通りあるか?」
これは、選んだ3人の「走る順番」も区別する必要があります(例:A君が1走とA君が2走は別)。
したがって、「順列(P)」を使います。
6人から3人を選んで並べるので、P(6, 3) となります。
計算式は 6 × 5 × 4 = 120通り です。
(もし「3人の代表を選ぶ」だけなら、順番は関係ないので「組み合わせ(C)」を使います。)
問題文を読んで、「順番に意味があるか?(順列P)」「順番は関係ないか?(組み合わせC)」を最初に見極めることが最も重要です。
詳しい解法やココシロのオリジナル練習問題は次の記事で紹介しています!
割合と比
「割合と比」は、「全体を100%(または1)としたとき、比べたい部分がどれだけか」を扱う問題です。
SPIでは「○は△の何%か?」といった計算や、比を使った問題が出ます。
例題
「ある大学の昨年の入学者は500人だった。今年は昨年より18%減少した。
この減少した人数は、文学部と理学部で 3 : 2 の比だった。
文学部の入学者減少数は何人か?」
まず、去年より減少した学生数を求めます。
昨年が500人なので、減少した人数は 500人 × 18% (0.18) = 90人 です。これが全体の減少数です。
この90人を、文学部と理学部で 3 : 2 の比で分け合っています。
比の合計は 3 + 2 = 5 です。
文学部の減少数は、90人のうち「5分の3」を占めるということです。
計算式: 90人 × (3 / 5) = 54人。
「A : B = 3 : 2」と出てきたら、「全体を (3+2)=5 と考える」というテクニックを身につけましょう。
「(部分)は(全体)の(割合)」という関係式を常に意識することが大事です。
損益算
「損益算」は、ビジネスの基本である「原価(仕入れ値)」「定価」「売価」「利益」の関係を計算する問題です。
「○割引き」や「利益率○%」といった言葉の意味を正確に捉えることが求められます。
例題
「原価800円の品物に、25%の利益を見込んで定価をつけた。しかし売れないため、定価から100円引きで売った。
このときの利益はいくらか?」
まず、定価を求めます。原価800円の25%(= 1/4)の利益を見込むので、利益は 800 × 0.25 = 200円 です。
定価 = 原価 + 利益 = 800円 + 200円 = 1000円。
次に、売価を求めます。定価1000円から100円引きで売ったので、売価は 1000円 – 100円 = 900円 です。
最後に、利益を求めます。利益 = 売価 – 原価 です。
900円 – 800円 = 100円。
「原価」「定価」「売価」の3つの言葉の違いを絶対に混同しないこと。
「25%の利益を見込む」は原価(800円)にかかり、「100円引き」は定価(1000円)にかかる、というように、「何に対しての割引・利益か」を丁寧に見極めましょう。
詳しい解法やココシロのオリジナル練習問題は次の記事で紹介しています!
料金割引
「料金割引」は、その名の通り、「○人以上で△割引」や「AプランとBプランどちらが安いか」といった、日常生活に近い料金計算の問題です。
例題
「ある施設への入場料は1人500円だが、10人を超える団体の場合、超えた人数分については1人300円になる。
15人の団体で入場する場合、入場料の総額はいくらか?」
15人の団体を、「10人までのグループ」と「10人を超えたグループ」に分けて考えます。
10人までのグループ:10人 × 500円 = 5000円。
10人を超えたグループ:15人 – 10人 = 5人。
この5人分の料金は1人300円になるので、5人 × 300円 = 1500円。
よって、総額は 5000円 + 1500円 = 6500円 となります。
問題文の条件が複雑に見えますが、情報を分けて整理することがすべてです。
「15人全員が300円」などと早とちりせず、「割引が適用されるのはどの部分か」を正確に読み取りましょう。
詳しい解法やココシロのオリジナル練習問題は次の記事で紹介しています!
仕事算
「仕事算」は、「ある仕事全体を終えるのに、Aさんなら○日、Bさんなら△日かかる。2人なら何日?」といった問題を解くものです。
例題
「ある仕事にAさんは3日、Bさんは6日かかります。
この仕事をAさんとBさんが協力し2人で行うと、何日かかりますか?」
仕事算の鉄則は、かかる日数の「最小公倍数」を仕事全体と置くことです。
Aさんは3日、Bさんは6日かかるので、3と6の最小公倍数である「6」を仕事全体の量とします。
Aさんが1日あたりにできる仕事量(能力)は、 6 ÷ 3 = 2 です。
Bさんが1日あたりにできる仕事量(能力)は、 6 ÷ 6 = 1 です。
2人が協力すると、1日あたりにできる仕事量は 2 + 1 = 3 です。
全体の仕事量「6」を、2人の1日あたりの仕事量「3」で割ると、かかる日数がわかります。
6 ÷ 3 = 2日。
「仕事全体を、かかる日数の最小公倍数(この場合は6)と置く」という解放を覚えることが最速の攻略法です。
分数を使わずに整数の計算だけで解けるようになるため、計算ミスがぐっと減りますよ。
詳しい解法やココシロのオリジナル練習問題は次の記事で紹介しています!
代金精算
「代金精算」は、複数の人が関わる支払いを計算する問題です。
「AがBの2倍多く払う」や「3人で割り勘にする」など、お金のやり取りを整理します。
例題
「A、B、Cの3人で食事に行き、合計9000円だった。
AはBより1000円多く、BはCより1000円多く支払うことにした。
Cさんが支払う金額はいくらか?」
こういう問題は、一番支払額が少ない人を「x」と置くのが基本です。
一番少ないCさんを「x円」とします。
BさんはCさんより1000円多いので、「(x + 1000)円」です。
AさんはBさんより1000円多いので、「(x + 1000) + 1000 = (x + 2000)円」です。
3人の合計が9000円なので、(x + 2000) + (x + 1000) + x = 9000 となります。
整理すると 3x + 3000 = 9000 → 3x = 6000 → x = 2000円。
「求めるもの(一番基準となるもの)をxと置く」という、中学1年生で習った方程式の基本がそのまま役立ちます。
焦って暗算せず、きちんと式を立てて整理しましょう。
速度算
「速度算」は、「速さ・時間・距離(み・は・じ)」の関係を使う問題です。
「追いかける」「出会う」「往復する」など、様々なパターンがあります。
例題
「P地点とQ地点は32km離れている。
Lさんは時速5kmでPからQへ、Mさんは時速7kmでQからPへ、同時に歩き始めた。
LさんとMさんが出会うのは、出発してから何時間何分後か?」
2人が互いに向かって進む場合、「2人の速さの合計」で距離が縮まっていきます。
1時間あたりに縮まる距離は 5km + 7km = 12km です。
32kmの距離を時速12kmで縮めていくので、出会うまでの時間は、
時間 = 距離 ÷ 速さ → 32km ÷ 12(km/時) = 32/12 = 8/3 時間 です。
「8/3 時間」を「何時間何分」になおします。 8/3 = 2 と 2/3 時間。
2/3 時間 = (2/3) × 60分 = 40分。
よって、答えは 2時間40分後 です。
「出会う」なら速さを足す、「追いかける」なら速さを引く、という基本パターンを覚えましょう。
「分」を「時間」になおす計算(例:15分 = 15/60 = 0.25時間)を瞬時にできるようにしておくことが重要です。
詳しい解法やココシロのオリジナル練習問題は次の記事で紹介しています!
集合
「集合」は、「英語が話せる人」「フランス語が話せる人」のように、複数のグループの重なりを計算する問題です。
SPIでは、2つまたは3つの円が重なる「ベン図」を使って解くのが鉄則です。
例題
「外国人200人にアンケートを行った。英語が話せる人は120人、フランス語が話せる人は40人いた。
英語とフランス語の「両方」が話せる人は25人いた。
このとき、英語とフランス語の「どちらか片方だけ」話せる人は何人か?」
ベン図(2つの円が重なった図)をイメージしてください。
「英語だけ」話せる人を求めます。英語が話せる120人から、両方話せる25人を引きます。
120人 – 25人 = 95人。
「フランス語だけ」話せる人を求めます。フランス語が話せる40人から、両方話せる25人を引きます。
40人 – 25人 = 15人。
「どちらか片方だけ」なので、この2つを合計します。 95人 + 15人 = 110人。
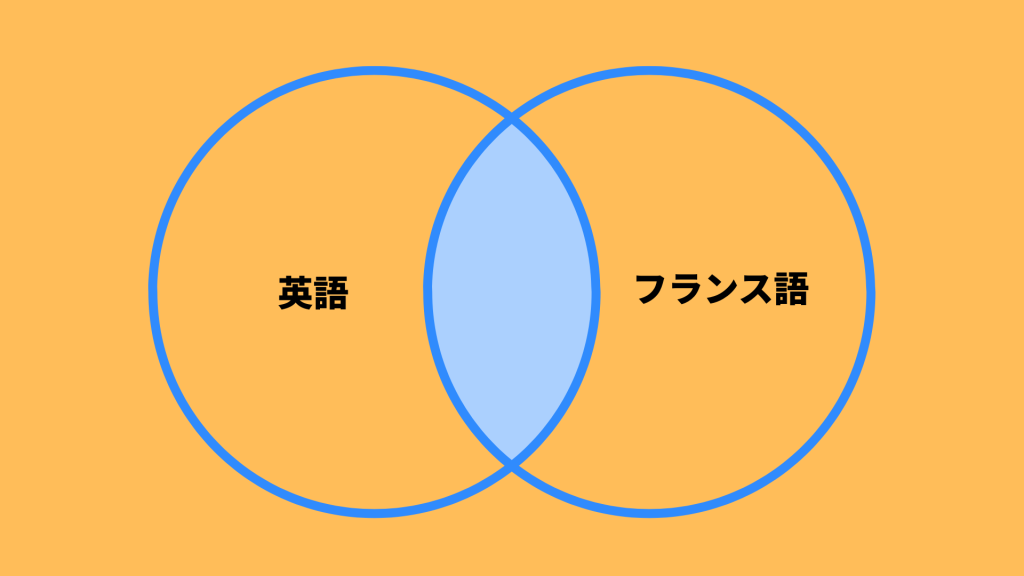
集合の問題が出たら、何も考えずにまず「ベン図」を大きく書くこと。
問題文の数字を、ベン図の「重なっている部分」なのか「外側の部分」なのか、正確に書き込むことができれば、必ず解けます。
詳しい解法やココシロのオリジナル練習問題は次の記事で紹介しています!
【難易度順】SPI非言語の難しすぎる問題3選

さて、10分野を一気に見てきましたが、その中でも特に「難しすぎる!」と就活生を悩ませるワースト3を紹介します。
これらは、なぜ難しいのか、その「難しいポイント」を知っておくだけでも対策がしやすくなりますよ。
1位:推論
難しいポイント:計算力ではなく「読解力」と「整理力」が求められる点。
推論は、他の問題のように「公式に当てはめればOK」という単純なものではありません。
「A > B」「CはDではない」「PとQは隣り合っている」といった複数の断片的な情報(条件)を、矛盾なく整理する必要があります。
問題文が長く、条件が複雑になればなるほど、頭の中だけで処理するのは不可能です。
情報を紙に書き出す、対戦表を作る、不等号で並べる、といった「自分なりの整理術」を確立していないと、時間をかけたのに結局解けないという最悪の事態に陥りやすいのです。
2位:確率
難しいポイント:「場合の数」の考え方が複合的に絡んでくる点。
確率は「(A) / (B)」で求められますが、この(A)(当てはまる場合の数)と(B)(すべての場合の数)を出すこと自体が難しいのです。
例えば「サイコロを3回振る」なら、すべての場合の数は 6 × 6 × 6 = 216通り と簡単です。
しかし、「A,B,C,D,Eの5人を並べる」場合の数は 5! = 120通り (順列)。
「5人から3人を選ぶ」場合の数は C(5,3) = 10通り (組み合わせ)。
このように、順列(P)と組み合わせ(C)の知識が曖昧なままだと、そもそも分母や分子を計算できず、手も足も出なくなってしまいます。
3位:集合
難しいポイント:情報の「重なり」を正確に把握するのが難しい点。
集合問題は、ベン図を使えば簡単ですが、使わないと地獄を見ます。
例えば「英語が話せる120人」という数字は、「英語『だけ』話せる人」と「英語『も』フランス語『も』話せる人」の合計です。
この「全体」と「部分」の関係を、問題文だけで読み解こうとすると、同じ人を二重にカウントしたり、逆に引くべきところを足してしまったりと、計算ミスが多発します。
特に円が3つ(例:英・仏・独)になった瞬間、重なりが複雑になり、パニックに陥りやすいのです。
難しすぎるSPI非言語の4ステップ対策法
「難しさ」の正体がわかったら、あとは対策あるのみです!
SPI非言語が苦手な人が、最短で結果を出すための「4ステップ対策法」をご紹介します。
①公式一覧を覚える
結局、非言語は「公式ゲーム」な側面があります。
「み・は・じ」「仕事算は全体を1」「損益算の利益=売価-原価」…。
こうした基本的な公式や解法パターンを覚えていないと、スタートラインにすら立てません。
まずは薄い問題集や参考書でいいので、主要な公式や解き方をざっと暗記してしまうこと。
ただし、暗記に時間をかけすぎず、大枠を掴んだら次のステップに進むのが「コツ」です。
思い出す作業が、一番の勉強になりますからね。
②自分の実力を知る
公式を覚えたら、いきなり分厚い問題集(青本など)に手を出すのは危険です。
難しすぎて挫折する原因No.1だからです。
まずは、「今の自分がどれくらい解けて、どの分野が苦手なのか」を正確に知る(自己分析する)ことが重要です。
そこでオススメなのが、ココシロインターンが提供する「5分5問でできる無料のSPI体験模試」です。
たった5分、5問だけで、あなたの「SPI非言語の現在地」がわかります。
「推論がヤバいかも」「速度算は意外と覚えてた」など、自分の実力を知ることで、③以降の勉強効率が劇的に変わりますよ。
SPI体験模試はこちら
③問題集で解法を理解する
自分の実力(と苦手分野)がわかったら、ようやく問題集の出番です。
何冊も買う必要はありません。
自分に合ったレベルの問題集を「1冊」だけ決めてください。
そして、まずは時間を気にせず、じっくり解いてみましょう。
間違えた問題は、「なぜ間違えたのか」「正解の解法(プロセス)は何か」を、解説を読んで完全に理解すること。
このステップでは、スピードよりも「解法のパターンを頭に叩き込む」ことが目的です。
④ひたすら練習問題を解く
解法をインプットしたら、最後はアウトプット、つまり「練習量」がモノを言います。
③で選んだその1冊の問題集を、最低3周は繰り返しましょう。
1周目は解法を理解するため。2周目は自力で解けるか試すため。3周目はスピードを意識するため。
3周目あたりでは、ストップウォッチを使い、「1問1分」を意識して時間を計りながら解くのが非常に効果的です。
体が「SPIのスピード感」に慣れてくれば、本番でも焦らず実力を発揮できるようになりますよ。
SPI非言語についてのよくある質問

最後に、就活生から寄せられる「非言語にまつわる不安な質問」に、ハッキリお答えします。
Q. SPI非言語がボロボロでした。落ちてますかね?
A. 「ボロボロ=即不合格」とは限りません。
確かに、大手企業や人気企業は、SPIの点数で足切りをしている可能性が高いです。
しかし、企業がSPIで何を見ているかは、本当に様々です。
「能力検査(非言語)はボロボロだと思ったけど、性格検査との相性が良くて通過した」というケースや、
「SPIよりES(エントリーシート)の内容を高く評価されて通過した」というケースもよくあります。
また、中小企業やベンチャー企業では、SPIを「あくまで参考程度」にしか見ていないことも。
なので、結果が出るまで諦めるのは早いですよ!
Q. SPI非言語が難しすぎます。捨ててもいいですか?
A. ダメです!でも、「完璧」を目指さなくてもいいんです。
非言語を「捨てる」(0点)のは、あまりにもリスクが高すぎます。
多くの企業が、面接に進むための「最低ライン」を設けているからです。
一般的に、SPIの合格ラインは6〜7割程度と言われています。
つまり、満点を取る必要は全くありません。
「難しい推論は後回しにして、簡単な損益算や速度算を絶対に取りこぼさない」という戦略が非常に重要です。
「全部捨てる」のではなく、「確実に取れる問題を増やす」という意識に切り替えて、基本的な分野だけでも対策しましょう。
まとめ
「難しすぎる」と感じるSPI非言語も、分解してみれば「解き方を知らない」だけだったりします。
今回の記事で、あなたの不安が少しでも軽くなれば嬉しいです。
- 非言語が難しい理由は「時間不足」「論理整理力」「出題範囲の広さ」。
- 対策の第一歩は「ベン図」や「公式」など、分野ごとの「解法パターン」を知ること。
- 対策は「①公式暗記 → ②実力診断 → ③解法理解 → ④反復練習」の4ステップが最強。
- 満点を狙わず、「6〜7割」を確実に取る戦略が大事。
まずは、あなたが「どの分野が苦手」で「今、何点くらい取れるのか」を知ることから始めましょう。
ココシロインターンの「SPI体験模試」なら、たった5分であなたの現在地がわかります。
自分の実力を知るのが、非言語攻略の最短ルートですよ!
SPI体験模試はこちら
人気記事























