SPIの非言語（数学）で、多くの就活生が「時間が足りない」「苦手だ」と感じるのが速度算です。
「公式は覚えたはずなのに、問題になると解けない」「単位変換でいつも混乱してしまう」といった悩みを抱えていませんか。
この記事では、SPIの速度算が苦手なあなたのために、基本的な公式の覚え方から、頻出パターンの具体的な解き方までを徹底的に解説します。
この記事を読めば、速度算への苦手意識がなくなり、本番でも自信を持ってスピーディーに問題を解けるようになります。
こんな人に読んで欲しい！
- SPIの速度算に強い苦手意識がある方
- 速度算の公式を覚えても、応用問題が解けずに悩んでいる方
- 限られた時間で効率よくSPI対策を進めたい方
SPIの速度算はなぜ難しい？
SPIの速度算は、限られた時間の中で「単位変換」や「問題文の読解」など、複数の処理を同時に行う必要があるため、多くの学生が難しく感じます。
速度算の問題は、単に公式を知っているだけでは解けません。
問題文から誰が、どこから、どの方向に、どんな速さで動いているのかを正確に読み取り、適切な公式と単位に当てはめる情報処理能力が求められるためです。
例えば、こんな問題があります。
【解答】
60秒
【解法】
電車の速さは時速90kmなので、秒速に直すと 90,000 ÷ 3600 = 25m/s になります。
トンネルの長さは1500mなので、電車が通過するのに必要な時間は、1500 ÷ 25 = 60秒 となります。
この問題では、速さの単位は「時速」、距離は「m」、答えは「秒」で求められています。こうした場合、計算を始める前に、すべての単位をmと秒に揃える「単位変換」という一手間が必要になります。
速度算を解く3つの鉄則
SPIの速度算を攻略するための鉄則は、「公式の完全理解」「単位変換の徹底」「情報の図式化」の3つです。
この3つを意識するだけで、解答のスピードと正確性が飛躍的に向上します。
鉄則①：公式は「き・は・じ」
速度・距離・時間の関係式は、小学校で習った「き・は・じ（み・は・じ）」の図で視覚的に覚えましょう。
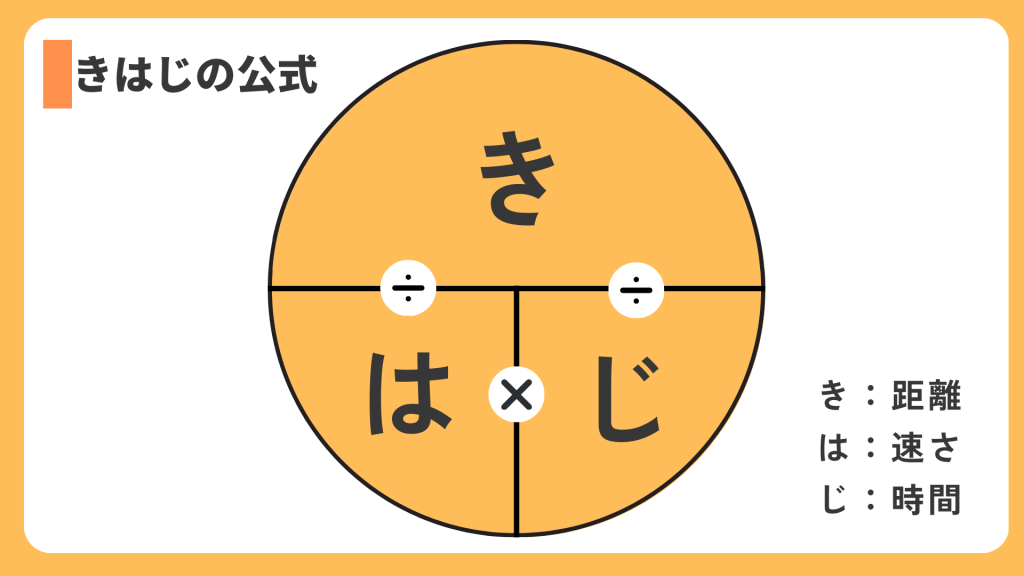
この図さえ覚えておけば、どの公式を使えばよいか一瞬で判断できます。文字の羅列ではなく、図として記憶しておくことで、思い出しやすくなり、ケアレスミスを防ぐことができます。
円の中に「き」「は」「じ」を書き、横線を割り算、縦線を掛け算と覚えます。
- 距離を求めたい場合：「き」を隠す → 速さ × 時間
- 速さを求めたい場合：「は」を隠す → 距離 ÷ 時間
- 時間を求めたい場合：「じ」を隠す → 距離 ÷ 速さ
この3つの公式はspi 速度算の全ての基本となるため、必ず完璧に覚えてください。
鉄則②：単位変換を制する
計算を始める前に、問題文中のすべての単位を揃えることを徹底してください。
特に「時速(km/h)」と「秒速(m/s)」の変換は頻出なので、暗記しておくと大幅な時間短縮になります。
速度算で最も多い失点原因が、単位のズレによる計算ミスです。
問題文にはわざと異なる単位が混ぜられていることが多いため、最初に単位を統一する一手間を惜しまないことが、正解への一番の近道です。
よく使う変換パターンは以下の通りです。
- 時間：1時間 = 60分 = 3600秒
- 距離：1km = 1000m
- 速さ：時速(km/h)から秒速(m/s)への変換は「÷ 3.6」、秒速(m/s)から時速(km/h)への変換は「× 3.6」と覚えておくと便利です。（例：時速72km = 72 ÷ 3.6 = 20m/s）
鉄則③：図を描いて情報を整理する
複雑な問題ほど、簡単な図や線分図を描いて情報を「見える化」しましょう。
図を描くことで、頭の中のワーキングメモリを節約し、計算に集中することができます。結果的に、解答時間の短縮とミスの減少につながります。
AさんとBさんが異なる地点から出会う問題であれば、一本の線分図を描き、両端にAとBを配置します。
それぞれの速さと進行方向を矢印で書き込むだけで、「2人の距離」と「近づく速さ（速度の和）」の関係性が直感的に理解できるようになります。
先輩が語る！速度算克服の体験談①
私は最初、問題集の難しい問題ばかり解いて、全然できずに落ち込んでいました。でもある時、基本に立ち返って「きはじの図を何も見ずに描けるか」「時速から秒速への変換を瞬時に言えるか」を自分に問いかけたら、意外と曖昧なことに気づいたんです。そこから1週間、毎日5分だけ図を描く練習と単位変換の暗唱を繰り返しました。すると、あれだけ複雑に見えた問題文が、どの公式と単位を使えばいいのかスッと頭に入ってくるようになったんです。（24卒・食品メーカー内定 Aさん）
SPIの速度算は、難しい数学的思考力よりも、基本的なルールを正確に素早く使えるかが問われます。そのため、焦って応用問題に手を出す前に、まずは「きはじの図」と「単位変換」を完璧にすることが大切です。
土台がしっかりしていれば、どんな問題にも落ち着いて対応できるようになります。
SPI速度算の頻出パターン4選
SPIの速度算には、「平均の速さ」「出会い算」「追いつき算」「通過算」という4つの頻出パターンがあります。
これらの解法パターンを覚えてしまえば、ほとんどの問題に対応できます。
これから、それぞれのパターンについて、解き方のポイントと具体的な例題を解説していきます。
パターン①：平均の速さ
【解答】
時速48㎞
【解法】
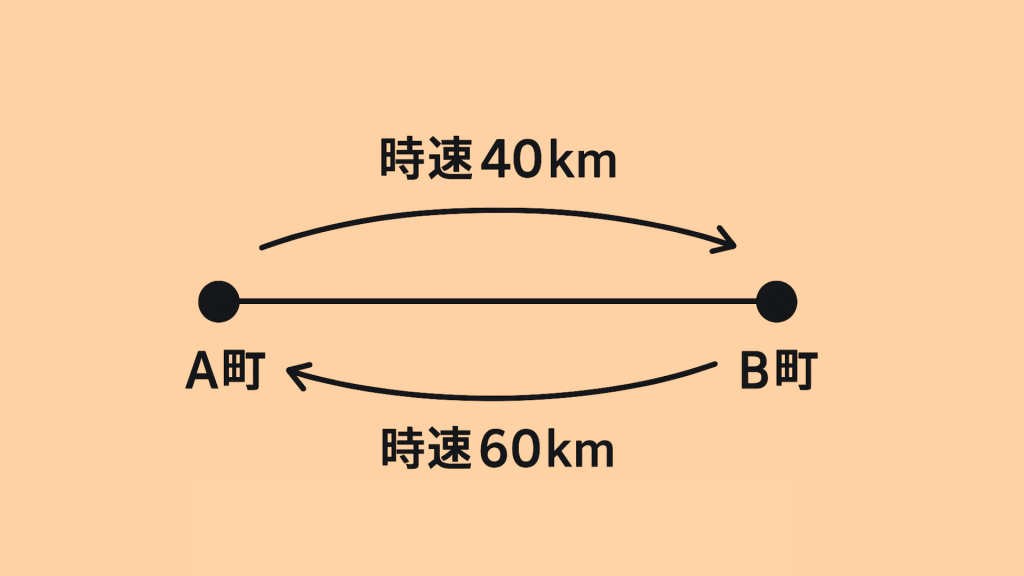
片道の距離を120km（40と60の最小公倍数）と仮定します。
・行きにかかる時間：120 ÷ 40 = 3時間
・帰りにかかる時間：120 ÷ 60 = 2時間
・全体の距離：120 × 2 = 240km
・全体にかかった時間：3 + 2 = 5時間
・平均の速さ：240 ÷ 5 = 48km/h。よって答えは時速48kmです。
平均の速さは、「全体の距離 ÷ 全体にかかった時間」で求めます。単純に速さの平均を取ってはいけない、という点に注意してください。
同じ距離でも、速さが異なればかかる時間が変わるため、単純な平均では正しい値を計算できません。
例えば、速く進んだ区間と遅く進んだ区間では、同じ距離でも滞在時間が異なるため、時間で重みづけをする必要があるのです。
パターン②：出会い算（旅人算）
【解答】
10分後
【解法】
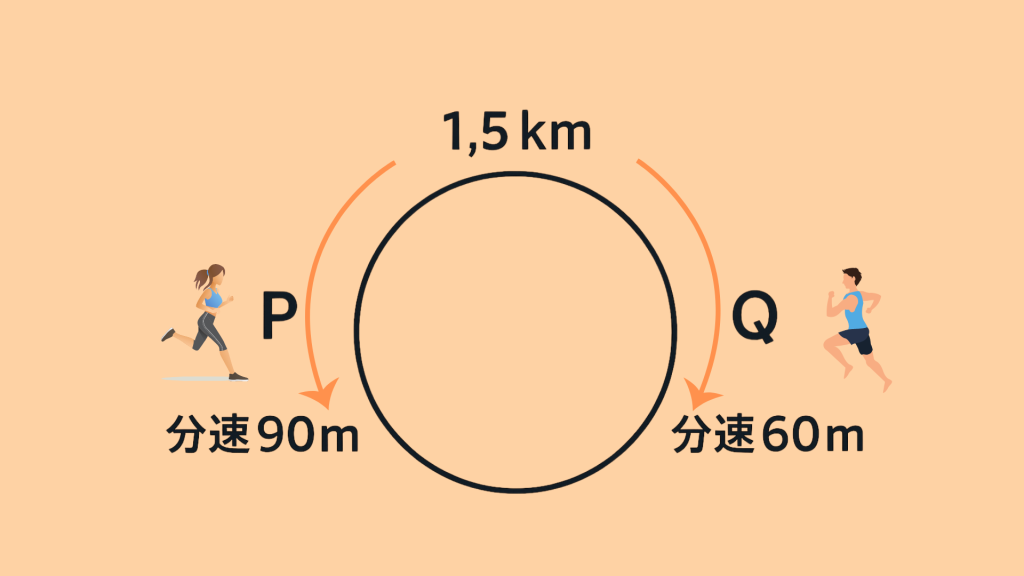
・2人の速さの和：90 + 60 = 150m/分（1分で150m近づく）
・2人の間の距離：1.5km = 1500m
・出会うまでの時間：1500 ÷ 150 = 10分。よって答えは10分後です。
2人が異なる場所から向かい合って進む「出会い算」は、2人の速さの「和」を使って計算します。
出会うまでの時間は、「2人の間の距離 ÷ 2人の速さの和」で求められます。
2人が向かい合って進むと、1時間あたり「Aの進む距離 + Bの進む距離」だけ、2人の間の距離が縮まります。
この「単位時間あたりに縮まる距離」が、2人の速さの和に相当するため、これを使って計算します。
パターン③：追いつき算（旅人算）
【解答】
20分後
【解法】
・兄が出発した時点で、弟が先に進んでいる距離：60m/分 × 10分 = 600m
・2人の速さの差：90 – 60 = 30m/分（1分で30m差が縮まる）
・追いつくまでの時間：600 ÷ 30 = 20分。よって答えは20分後です。
同じ方向に進む2人の「追いつき算」は、2人の速さの「差」を使って計算します。
追いつくまでの時間は、「最初に離れている距離 ÷ 2人の速さの差」で求められます。
速い方が遅い方に追いつくためには、1時間あたり「速い方の進む距離 – 遅い方の進む距離」だけ、2人の間の距離を縮める必要があります。
この「単位時間あたりに縮まる距離」が、2人の速さの差に相当するため、これを使って計算します。
パターン④：通過算
【解答】
40秒
【解法】
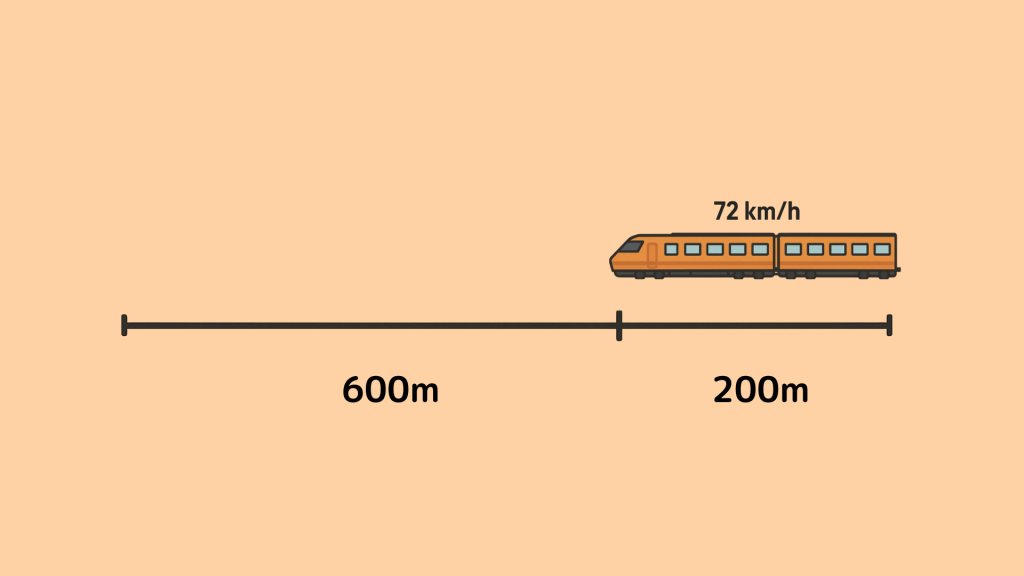
・速さの単位変換：時速72km = 72 ÷ 3.6 = 20m/s
・電車が移動する総距離：200m (電車の長さ) + 600m (鉄橋の長さ) = 800m
・かかる時間：800 ÷ 20 = 40秒。よって答えは40秒です。
電車がトンネルなどを通過する「通過算」では、移動距離が「(電車の長さ) + (トンネルの長さ)」になるのがポイントです。
電車の先頭がトンネルに入ってから、最後尾がトンネルを完全に出るまでの距離を考えます。
通過の完了とは、電車の最後尾がトンネルの出口を通過した瞬間を指します。
そのため、電車の先頭が移動した距離は、トンネルの長さに加えて、電車自身の長さ分も進んでいることになります。
先輩が語る！速度算克服の体験談②
兄が弟を追いかける問題で、出発時間が違うパターンが本当に苦手でした。頭の中がごちゃごちゃになって、いつもパニックに。でも、キャリアセンターの先輩に「兄が出発する瞬間の、2人のスナップショットを図に描いてごらん」とアドバイスされたんです。弟が先に進んだ距離を線で描き、そこから兄が追いかける構図にしたら、「ああ、この距離を速さの差で割ればいいだけなんだ」と腑に落ちました。それ以来、どんな問題でもまず状況を図に描くクセをつけたら、正答率が劇的に上がりました。（24卒・ITコンサル内定）
一見難しそうに見える問題も、分解すれば基本パターンの組み合わせに過ぎません。
問題文のどの部分が「最初の距離」で、どの部分が「速さの差」になるのかを図で整理することで、解法の糸口が見えてきます。
効率的なSPI問題の勉強法
SPIの効率的な勉強法は「①1冊の問題集を完璧にする」「②苦手分野を潰す」「③時間を計って解く」の3つです。やみくもに手を広げるより、一つの教材を繰り返し解く方が効果的です。
まずは問題集を1周して、自分の苦手分野（推論、長文読解など）を把握します。次に、その苦手分野を重点的に2周、3周と繰り返し解き、解法パターンを体に染み込ませましょう。通学中などのスキマ時間には、無料アプリで語彙問題などを解くのもおすすめです。
また、力試しにSPI体験模試を受けてみるのもおすすめです。
基本的にSPIは結果が確認することのできないですが、SPI体験模試では各分野の結果を確認することができます！
「SPIの模試を受けたい」「SPIの結果を確認したい」と感じた方は、「SPI体験模試」に挑戦してみることをおすすめします！
SPI体験模試では、
- 本番同様の時間制限下で解ける
- 適性検査の結果から自分の実力がわかる
- 各問題の解説がじっくり見られる
など、結果を確認できるからこそ、あなたの就活を効率的に進めることができます。
「SPI体験模試」はこちらから！
SPI体験模試はこちら
SPIの受験まで時間がない！という方は、こちらの記事を参考にしてみてください。
SPIの先にある、本当の自己分析
SPI対策は就活の重要なステップですが、それと同時に「自分はどんな仕事がしたいのか」という自己分析を深めることも大切です。
自分の強みや価値観を明確にすることで、入社後のミスマッチを防ぐことができます。
SPIの点数が高くても、自分の適性に合わない企業に入社してしまっては、早期離職につながりかねません。
就職活動のゴールは内定を得ることではなく、自分らしく輝ける場所を見つけることだからです。
SPIの勉強は大変だけど、そもそも自分はどんな業界に行きたいんだろう？
自分のどんな強みを活かして働きたいんだろう？
そんな風に感じたら、一度立ち止まって自己分析をしてみませんか？
以下の「自己分析シート」を使えば、質問に答えていくだけで、あなたの強みや価値観、やりたいことが言語化できます。SPI対策の合間に、ぜひご活用ください。
自己分析シートを利用するにはこちらをクリック
まとめ：SPI速度算はパターンで攻略
最後までお読みいただきありがとうございます。この記事の内容をまとめと次のようになります。
- 鉄則：計算前に「単位」を揃え、「公式」を思い出し、「図」を描いて整理する！
- パターン：「平均速度」「出会い算」「追いつき算」「通過算」の解き方を覚えれば、ほとんどの問題に対応できる！
- 練習：苦手分野は問題集で繰り返し解き、体に覚えさせるのが一番の近道！
SPIの速度算は、3つの鉄則（公式、単位、図）を徹底し、4つの頻出パターン（平均、出会い、追いつき、通過）をマスターすれば、必ず得意分野にできます。
繰り返し問題を解いて、解法を体に覚えさせましょう。
速度算は、ひらめきではなく、正しい手順と知識の積み重ねで解ける問題です。
練習を重ねることで、問題を見た瞬間に解法パターンが頭に浮かぶようになり、時間内に焦らず解ききることができます。
この記事が少しでも皆さんのお役に立てば幸いです。
基本的にSPIは結果が確認することのできないですが、SPI体験模試では各分野の結果を確認することができます！
「SPIの模試を受けたい」「SPIの結果を確認したい」と感じた方は、「SPI体験模試」に挑戦してみることをおすすめします！
SPI体験模試では、
- 本番同様の時間制限下で解ける
- 適性検査の結果から自分の実力がわかる
- 各問題の解説がじっくり見られる
など、結果を確認できるからこそ、あなたの就活を効率的に進めることができます。
「SPI体験模試」はこちらから！
SPI体験模試はこちら