【SPI対策】速度算を3つのパターン別で図解！

SPIの非言語で多くの就活生がつまずく「速度算」。

「意味わかんない…」「時間が足りなくていつも焦る…」なんて悩んでいませんか？

しかし実は、速度算はいくつかのコツと解き方パターンさえ押さえれば、誰でも確実に正解できるようになります。この記事では、速度算の基本から応用まで、分かりやすく解説していくので、ぜひ最後まで読んでみてくださいね！

こんな人に読んでほしい

SPIの速度算に苦手意識があって、どうにかしたい人
テスト本番で、計算問題を早く正確に解けるようになりたい人
非言語で安定して点数をとって、周りと差をつけたい人

目次閉じる

そもそも速度算とは
- 速度算が苦手な就活生は多い
速度算を解く時の3つのコツ
速度算の解き方をパターン別で図解
非言語分野はこの2ステップで完璧
- 1. 「SPI体験模試」で苦手分野を把握
- 2. 苦手分野を問題集で繰り返し解く
速度算の練習問題6選
まとめ

そもそも速度算とは

速度算とは、SPIの非言語分野で出題される「速さ・時間・距離」に関する文章問題のこと。一見すると複雑そうですが、実は小学校で習った算数の応用なので、基本をしっかり思い出せば大丈夫です。

速度算が苦手な就活生は多い

「速度算、マジで苦手…」と感じていても、安心してください。あなただけではありません。Xから集めてきた就活生の声を見てみましょう。

就活生A

SPIむずいいいいい！速度算が1番苦手

就活生B

最近SPIの勉強してるんだけど、ほんと速度算とか苦手だ……

点Pから5分後とかに出発すんな。

就活生C

spiの問題集ってなんで推論から始まるの？ webテストは大体簡単な(私にとっては簡単じゃない)速度算とかから始まるのに

確かに、限られた時間で問題文を正確に読み取り、公式を当てはめて計算するのは、想像以上に難しいですよね。

特に、登場人物が2人になったり、単位がバラバラだったりすると、頭がこんがらがってしまうのも無理はありません。でも、多くのライバルが苦手としているからこそ、ここをマスターすれば大きなアドバンテージになります。

速度算を解く時の3つのコツ

本格的な解き方パターンに入る前に、まずは絶対に押さえておきたい3つの基本のコツを紹介します。この3つを意識するだけで、ケアレスミスが劇的に減り、正答率が安定しますよ。

1. 単位変換に気をつける

速度算で一番やりがちなミスが、実は単位のズレです。問題文に「時速（km/h）」と「分」や、「km」と「m」が混ざっていたら超要注意。

計算を始める前に、速さ・時間・距離の単位をどれか一つに揃えるクセをつけましょう。例えば、時速を分速に直したり、分を時間に直したりする一手間を惜しまないでください。これを意識するだけで、正解率はグッと上がります。

時間の単位変換

【1時間=60分、1分=60秒】です。たとえば「2時間」は「2×60＝120分」、「90秒」は「90÷60＝1.5分」として計算します。

距離の単位変換

【1km=1000m、1m=100cm】です。たとえば「2.5km」は「2.5×1000＝2500m」、「150cm」は「150÷100＝1.5m」になります。

速さの単位変換

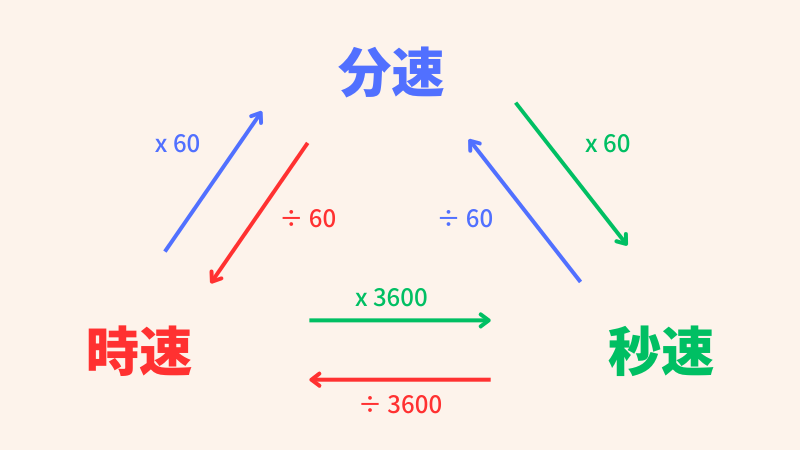
速さの単位変換は、「距離」と「時間」の両方の単位をそろえることが大切です。たとえば「分速」を「時速」に直すには、60倍します（1時間＝60分だから）。逆に「時速」を「分速」にするときは60で割ります。

2. 公式を暗記する

次に、言うまでもなく公式の暗記です。速度算は、道具である公式を知らないと絶対に太刀打ちできません。

ここで思い出すべきなのが、小学校で習った「き・は・じ」の法則です。「距離」「速さ」「時間」の関係性を忘れてしまったら、この図を思い出してください。

・距離 = 速さ × 時間
・速さ = 距離 ÷ 時間
・時間 = 距離 ÷ 速さ

3. 情報を分かりやすく整理する

問題文がゴチャゴチャしてて、何が何だか分からなくなること、ありますよね。そんな時は、頭の中だけで考えようとせず、手を動かすのが一番です。

とにかく簡単な図や表を書いて、情報を整理するのが1番の解決策。誰が、どこから、どのくらいの速さで動いているのかを「見える化」するだけで、問題の構造がクリアになります。この一手間が、結果的に時間を短縮し、正解への最短ルートを示してくれます。

速度算の解き方をパターン別で図解

速度算の問題は、実はたった数種類の出題パターンに分類できます。ここでは、最頻出の3つのパターンについて、解き方のポイントを図解付きで解説します。この型さえ覚えてしまえば、怖いものなしです！

パターン1：平均速度

「行きは時速40km、帰りは時速60km。平均の速さは？」というような平均速度を求めるタイプの問題です。ここで、単純に(40+60)÷2=50km/hと計算するのは典型的な間違いなので絶対にやめましょう。

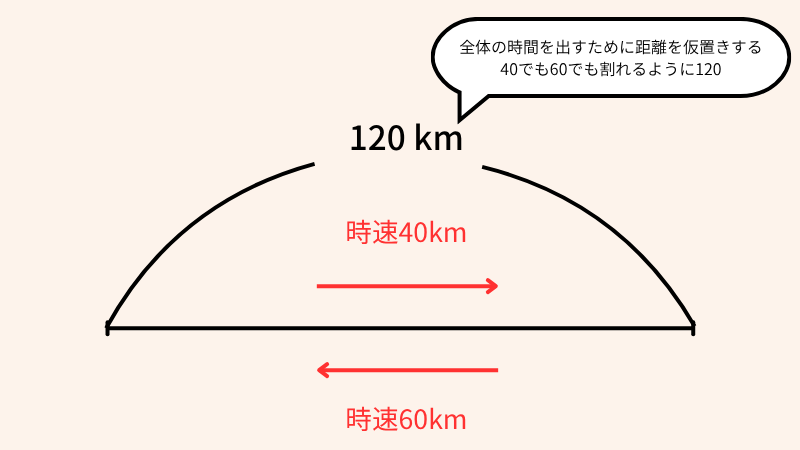
平均速度の正しい求め方は、「全体の距離 ÷ 全体にかかった時間」です。この鉄則さえ守れば、どんな問題でも解けます。例えば、片道の距離を適当な数字（速さの最小公倍数など）に設定して、行きと帰りの時間をそれぞれ計算し、公式に当てはめればOKです。

距離を決める（計算しやすく）
→ 片道120km（40と60の最小公倍数）
時間を出す
行き：120 ÷ 40 = 3時間
帰り：120 ÷ 60 = 2時間
全体の距離と時間
全体の距離：120 × 2 = 240km
全体の時間：3 + 2 = 5時間
平均速度を計算
→ 240 ÷ 5 = 48km/h

パターン2：出会い算

「A君とB君が、10km離れた地点から向かい合って同時に出発します。A君は時速4km、B君は時速6kmで進む時、2人が出会うのは何分後？」といった出会う時刻を求めるタイプの問題です。

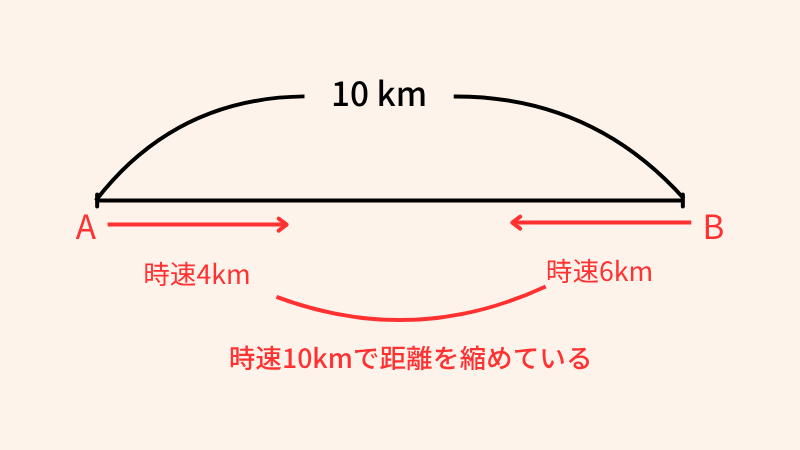
このパターンのポイントは、2人の速さを足し合わせること。2人が向かい合って進む場合、1時間で縮まる距離は「A君が進む距離＋B君が進む距離」になりますよね。つまり、2人の速さの合計が、距離が縮まる「相対的な速さ」になるわけです。

したがって、出会うまでの時間は「2人の間の距離 ÷ (速さA + 速さB)」というシンプルな式で求められます。「向かい合って進むなら速さはプラス！」と覚えてしまいましょう。

出発時の距離：10km
距離が縮まる速さ（相対速度）：時速4km + 時速6km = 時速10km
出会うまでの時間：10km ÷ 時速10km = 1時間

パターン3：追いつき算

「弟が家を出て分速60mで歩き始めた10分後に、兄が分速160mの自転車で追いかけました。兄が弟に追いつくのは何分後？」というような、追いつく時間を求めるタイプの問題です。

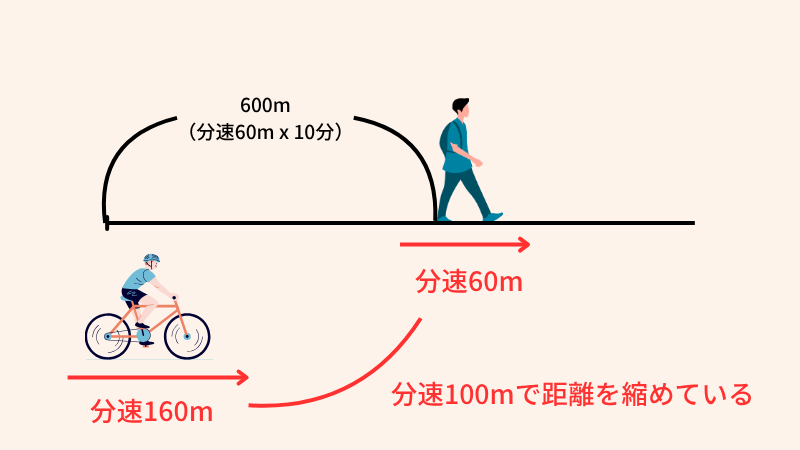
これも「出会い算」と考え方は同じ。ポイントは、速い方の速さから遅い方の速さを引き算すること。兄が弟に1分間でどれだけ距離を詰められるかは、「兄の速さ – 弟の速さ」で計算できますよね。これが追いかける時の「相対的な速さ」です。

追いつくまでの時間は、「最初に離れている距離 ÷ (速い方の速さ – 遅い方の速さ)」で求められます。最初に弟が10分間で進んだ距離を計算し、それを速さの差で割れば答えが出ます。「追いかけるなら速さはマイナス！」と覚えましょう。

最初の距離を求める
弟は兄より10分早く歩き始めています。
→ 弟が10分で進む距離：分速60m × 10分 = 600m
速さの差を出す（相対速度）
兄と弟の速さの差：分速160m − 分速60m = 分速100m
追いつくまでの時間を求める
600m ÷ 分速100m = 6分

非言語分野はこの2ステップで完璧

ここまで速度算の解き方を解説してきましたが、SPIの非言語分野全体を攻略するには、効率的な学習戦略が不可欠です。闇雲に問題を解くのではなく、この2ステップで対策を進めるのがおすすめです。

1. 「SPI体験模試」で苦手分野を把握

まず最初にやるべきは、本番と同様の形式でを一度問題を解いてみることです。これによって、自分の実力と苦手分野を正確に把握することができます。

おすすめなのは、「SPI体験模試」です。この模試では本番と同様に時間制限がある状態でSPIの問題を解くことができます。また、問題数も少ないので短い時間で効率的に自分の苦手分野を把握することができるのです。

「自分は速度算が苦手だと思っていたけど、実は確率の方がヤバかった…」なんて発見があるかもしれません。最初に弱点を特定することで、その後の学習をピンポイントで行えるため、無駄な時間を大幅にカットできます。受験は下のボタンからすぐにできますよ。

SPI体験模試はこちら

SPI体験模試を受ける

2. 苦手分野を問題集で繰り返し解く

自分の苦手分野が分かったら、あとはその分野を問題集で徹底的に潰すだけです。参考書を1冊買ってきて、苦手な章の問題を、解法を見なくてもスラスラ解けるようになるまで何度も繰り返しましょう。

同じパターンの問題を何度も解くことで、解法が体に染み付いていきます。「あ、この問題、問題集で解いたやつだ！」という状態になれば、本番でも焦らず、自信を持って計算を進められるはずです。

次の記事では、SPIにおすすめな対策本を一挙に紹介しているので、ぜひ参考にしながら自分にあった対策本を選んでみてください！

速度算の練習問題6選

それでは、ここまでの内容を定着させるために、実践的な練習問題にチャレンジしてみましょう！各パターンの問題を2問ずつ用意しました。

問題①：平均速度

A町からB町まで、行きは時速30km、帰りは時速60kmで往復した。この時の平均速度は時速何kmか。

解答・解説

距離が設定されていないので、計算しやすいようにA町からB町までの距離を、2つの速度（30と60）の最小公倍数である60kmと仮定するのが楽です。

1. 行きにかかる時間： 60km ÷ 30km/h = 2時間
2. 帰りにかかる時間： 60km ÷ 60km/h = 1時間
3. 往復の平均速度：
全体の距離は 60km + 60km = 120km
全体にかかった時間は 2時間 + 1時間 = 3時間
よって、120km ÷ 3時間 = 時速40km

問題②：平均速度

A地点から60km離れたB地点まで時速20kmで進み、B地点で30分休憩した後、B地点から30km離れたC地点まで時速30kmで進んだ。A地点からC地点までの平均速度は時速何kmか。

解答・解説

休憩時間も「全体にかかった時間」に含めて計算するのがポイントです。単位を「時間」に揃えるのを忘れずに！(30分 = 0.5時間)

1. A→Bの時間： 60km ÷ 20km/h = 3時間
2. B→Cの時間： 30km ÷ 30km/h = 1時間
3. 全体の時間： 3時間 + 0.5時間(休憩) + 1時間 = 4.5時間
4. 全体の距離： 60km + 30km = 90km
5. 平均速度： 90km ÷ 4.5時間 = 時速20km

問題③：出会い算

周囲が1.8kmの池の周りを、Aさんは分速70m、Bさんは分速80mで、同じ地点から反対方向に向かって同時に出発した。2人が初めて出会うのは、出発してから何分後か。

解答・解説

反対方向に進むので、2人の速さを足し合わせます。単位を「m」に揃えましょう。(1.8km = 1800m)

1. 2人の速さの和： 70m/分 + 80m/分 = 150m/分
（1分間で2人の間の距離が150m縮まる、ということ）
2. 出会うまでの時間： 1800m ÷ 150m/分 = 12分後

問題④：出会い算

A君の家とBさんの家は1本道で2km離れている。A君が分速80mでBさんの家に向かって出発した。その5分後に、Bさんが分速70mでA君の家に向かって出発した。2人が出会うのは、A君が出発してから何分後か。

解答・解説

出発時刻が違うのがポイント。Bさんが出発した時点で、2人はどれだけ離れているかを考えます。(2km = 2000m

1. A君が5分間で進んだ距離： 80m/分 × 5分 = 400m
2. Bさん出発時点での2人の距離： 2000m – 400m = 1600m
3. 2人が同時に進み始めてから出会うまでの時間：
速さの和は 80 + 70 = 150m/分なので、
1600m ÷ 150m/分 = 160/15分 = 32/3分
4. A君が出発してからの合計時間：
先に進んだ5分 + 32/3分 = 15/3 + 32/3 = 47/3分後

問題⑤：追いつき算

弟が家を出て分速60mで歩いて駅に向かった。その12分後に、姉が自転車に乗って分速180mで同じ道を追いかけた。姉が弟に追いつくのは、姉が出発してから何分後か。

解答・解説

追いかけるので、2人の速さの差で距離を詰めていきます。

1. 姉が出発する時点で弟が先に進んでいる距離：
60m/分 × 12分 = 720m
2. 2人の速さの差： 180m/分 – 60m/分 = 120m/分
（1分間で120mずつ追いついていく）
3. 追いつくまでの時間： 720m ÷ 120m/分 = 6分後

問題⑥：追いつき算

A君はP地点から時速5kmで歩き出し、B君はA君が出発した1時間後に、P地点から8km離れたQ地点から時速9kmでA君と同じ方向に歩き出した。B君がA君に追いつくのは、B君が出発してから何時間後か。

解答・解説

出発地点も時刻も違う、少し応用的な問題です。B君が出発する瞬間の2人の位置関係を整理しましょう。

1. B君が出発する時（A君出発の1時間後）、A君はどこにいる？
A君は時速5kmなので、P地点から5km進んでいます。
2. その時の2人の間の距離は？
A君はP地点から5km前方、B君はP地点から8km後方。つまり2人の間の距離は 8km + 5km = 13km です。
3. 2人の速さの差： 9km/h – 5km/h = 4km/h
4. 追いつくまでの時間： 13km ÷ 4km/h = 3.25時間
3.25時間をわかりやすい形に直すと、答えは 3時間15分後 です。